Binary Search Algorithm
Binary search algorithm which is also known as the logarithmic algorithm is an algorithm and it is used in finding an item from the sorted array. The binary search algorithm is faster than a linear search algorithm. Make sure you remember that the array must be sorted for the algorithm to work. You will understand why the array should be sorted as you go through the article.
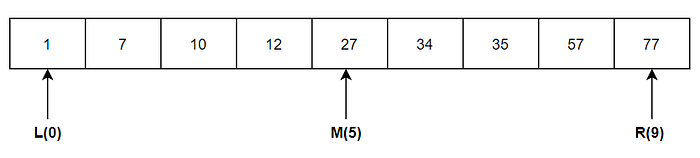
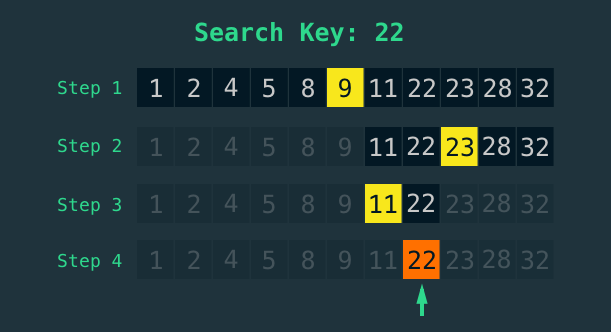
Let us consider a sorted array of length N. Assume three indices one is the left index(L), one is the right index(R), and the middle index (M) is the floor value of (L+R)/2. For example, if L+R is 9, then the value of 9/2 is 4.5 and the floor value is 4.
Steps:
- Divide the algorithm into two chunks and the least index is the left index, the highest index is the right index R and the middle index is calculated by the above formula floor((L+R)/2).
- Check if the value of the array in mid-index (array[M]) is equal to the searched value. If the value is found, return the mid-index.
- Consider the item to search, if the item is higher than the value of the array in mid-index (array[M]), move the left index to the right of mid-index.
- Consider the item to search, if the item is lesser than the value of the array in mid-index (array[M]), move the right index to the left of mid-index.
- Do the steps from 1 to 4 recursively until you find search value is equal to (array[M]).
- In some cases, the value you search may not be found in the array. At that time, stop searching when the left-index L is greater than the right-index R (L > R).
To make it short there are only three cases that can occur when you search for an element in an array which is given below:
- value = array[M]
- value < array[M]
- value > array[M]
Move the left and right pointer based on the situation you encounter and know when to stop (L > R).
Python Code for Binary Search Algorithm.
import math
def search(val, arr ):
n = len(arr)
l = 0
r = n-1
while l<=r:
m = math.floor((l+r)/2)
if val==arr[m]:
return m
elif val<arr[m]:
r = m-1
elif val>arr[m]:
l = m+1
return "not found"print(search(4, [0, 1, 2, 3, 4]))
Complexity:
The worst case complexity of the linear search is O(n) because you have to search through the whole array when the element you search is at the end of an array. The worst case complexity of the binary search is O(log n) because the search space is reduced everytime when you search through the array.
Interesting Info: https://www.codementor.io/@ashwanitr001/is-your-binary-search-bug-free-16ptximygu